Trong bài viết này chúng ta sẽ cùng nhau đi tìm hiểu xem thế nào là hình nón cụt, công thức tính diện tích hình nón cụt trong toán học lớp 9 ra sao để vận dụng giải các bài toán khó trong hình học.
Khái niệm hình nón cụt là gì
Hình nón cụt được tạo ra từ hình nón như sau: cho tam giác AOC vuông ở O. Khi quay tam giác vuông này một vòng quanh cạnh OA ta sẽ được một hình nón. Cạnh OC quét đáy tạo thành một hình tròn tâm O bán kính OC. Trong khi đó, cạnh AC quét tạo thành mặt xung quanh của hình nón và cạnh AC được gọi là đường sinh của hình nón.
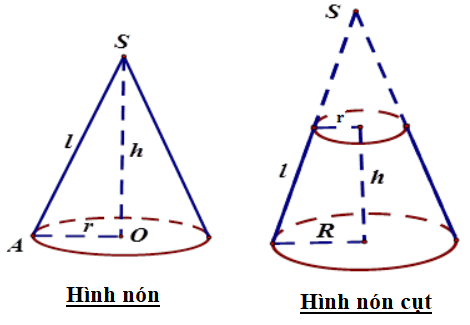
Từ hình nón đã được tạo thành, ta dùng một mặt phẳng song song đáy cắt qua hình nón, ta được một hình nón cụt.Như vậy, hình nón cụt là hình có 2 đáy là hai hình tròn có bán kính to nhỏ khác nhau nằm trên hai mặt phẳng song song có đường nối tâm là trục đối xứng.
Khái niệm hình quạt tròn? Cách tính diện tích hình quạt tròn và bài tập
Hình tam giác là gì? cách tính diện tích các hình tam giác
Định nghĩa tỉ số lượng giác của góc nhọn, công thức và phương pháp giải
Công thức tính thể tích hình nón cụt
Giả sử ta có hình nón cụt với r1 và r2 lần lượt là bán kính hai đáy của hình nón cụt, h là chiều cao và l là độ dài đường sinh.
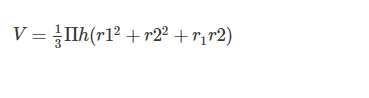
Cách tích diện tích xung quanh của hình nón cụt
Bên cạnh thể tích hình nón cụt, công thức tính diện tích xung quanh cũng là một công thức quan trọng không thể bỏ qua.
Ta có cách tích thể tích hình nón cụt:


Dạng bài tập bán kính nhỏ của hình nón cụt
Cho hình nón cụt có bán kính lớn r2= 12cm, đường cao h=8cm và độ dài đường cao l=10cm. Tính độ dài đường kính nhỏ và diện tích xung quanh, thể tích hình nón cụt.
Hướng dẫn:
Với dạng bài tập này, ta vẫn tiếp tục sử dụng định lý Py-ta-go để tính độ dài đường kính nhỏ:
Gọi độ dài đường cao l= AB = 10cm, đường kính lớn O’B= r2 = 12cm và đường cao OO’= h = 8cm.
Gọi bán kính nhỏ r1= OA và h là chân đường vuông góc hạ từ A xuống O’B.


Xem thêm :
Hàm số bậc nhất là gì? Định nghĩa và tính chất của hàm số
